Optimizing the eviction of code containers from disk

The code for the experiments and data hydration that I mention in this post is available here.

I’m working on a system to run code on demand (hint), and so I’m always thinking about the current and future architectures of this system, things that may happen in the future and ways I can react to them, possible ways to expand the system, how I can further simplify what I already have, and so on.

At the end of August, I came across Juncheng Yang’s post about his work on S3-FIFO, a new cache eviction algorithm. This made me focus on one of the things I had been thinking about. In this code-on-demand system (I’ll also refer to it as “the system” throughout this post), machines receive some input to work on, along with a reference to the code that needs to run. To do the work, they need to fetch the code from a repository, and then run that code with the given input. If this system keeps going forever as described, and assuming the system gets a lot of different pieces of code to run over time, a machine will run out of disk space, because its disk will get full of code that it had to run at some point, but doesn’t need to anymore. A solution to this problem involves cleaning up old, unneeded code. This resembles cache eviction, and I wondered whether I could adapt S3-FIFO to work in this scenario.

Since the system functions similarly to every other Function-as-a-Service system out there, I did some light searches for publications on this eviction mechanism, but couldn’t find anything interesting, even after getting some good pointers from Juncheng. Almost every result talked about the optimization of cold-start latencies (in most cases by keeping the code running), which is related to the scenario I had in mind, but still not the exact thing: the system still has to fetch code in certain cases, and optimising this particular step is what I’m interested in.

Evicting code in the system

When a machine receives a signal to run some code, it needs to first fetch the code that it needs to run. The machine stores the code on disk, and keeps it there while the code runs. It could also just keep the code in-memory and remove it from disk (or never write it there to begin with), but in practice this behaviour would help in rare cases, while making all normal cases less efficient (and introducing tricky cases when code is dynamically loaded as it runs). For example, given that the system knows that a machine has the code already cached on disk, it can route extra requests for the same code to that same machine, because it won’t need to fetch the code from the repository again. This “optimisation” (more like common sense tbh) improves the performance of the system quite a bit: code starts up faster, and the system also minimizes the amount of code pulls from a repository, thus better utilising the network with other data instead of filling it with duplicate requests for code packages/images. Because of this, it’s better to start with the assumption that code won’t ever get removed while it’s still running.

The need for eviction arises because we want to cache code in the local disks of the machines, which means that at some point we need to remove older code that hasn’t run in a while so we can make space for newer code. This scenario is a bit special though, because we also don’t want to remove code that is running on the machine. This means that for some period of time, we have entries in our cache that we just can’t remove at all. After some light search, I haven’t found eviction algorithms that work with this constraint, so the bulk of the work I did was to try adaptations that introduce this constraint in existing algorithms. I explain the adaptations that I made in a later section.

While working on those adaptations, I also figured out that we can approach this problem in a different way: since we don’t want to evict running code, we can just wait until it has finished running before adding it to our eviction queue (it will already be in the cache, just not eligible for eviction yet). Basically, the size of our eviction queue becomes “dynamic”: if our queue is at 10GB and a signal comes in to run some code weighing 1GB, the queue shrinks to 9GB. Similarly, if some code weighing 1GB finishes running, the queue grows by 1GB (and the extra 1GB will “instantly” fill up with the code that just finished running). This allows the use of existing eviction algorithms without introducing a new constraint. Dynamically resizing the queue size is often easier than making existing items unremovable, because reducing the queue size means we just need to evict more items until the queue is at or below the target size, and increasing the size is almost instant with not a lot of extra work needed.

Since we can’t remove some items from the cache until they’re finished running, the cache can also become overfilled: it can hold enough pieces of code running at the same time that we can’t add any more, because that would exceed its size. In practice, this is probably never going to happen because disk space is plenty, but CPU and RAM aren’t, so the machine will become too busy before its disk becomes too full. The system doing the work distribution should also know how “full” any machine is to avoid this issue.

As implied before, the way that the system distributes work between machines affects how well a machine can reuse the code it already has in its local cache. Because of that, it’s important to test the system as a whole when comparing the performance of cache eviction algorithms. As I don’t yet have a production-ready system, I assumed a single machine running all invocations. I had this itch to scratch, and I couldn’t wait until I had something more proper months down the line. Since I was assuming a single machine running all invocations, for each experiment I had to calculate the minimum size required for the cache so I could finish the experiment without overfilling it. The minimum size is equal to the largest sum of disk space used by invocations at any time.

Finding some data for experiments

Given the lack of literature on this problem, I wondered how I could experiment with the algorithm adaptations I was thinking about. The system I’m working on is still not in production, but I wanted production-like traffic to experiment with my ideas. After digging through the Internet, I also found zero datasets that had everything I needed to run some experiments.

The data I needed is simple. With an identifier for the code/function to run, a timestamp indicating when it started, a duration (or a timestamp indicating when it finished), and the size of the code, I could write some code that goes over the data and gives me some data about the performance of every adaptation (when I talk about the results from my experiments in a later section, this is essentially what an experiment consists of). Most datasets provided the first 3 pieces of data I needed, and maybe some extra information such as CPU and memory usage, which didn’t help me that much. The best “open” dataset that I found was the Azure public dataset (you’ll understand the reason for the quotes in the next section).

That dataset contains two collections that interested me: a trace of function invocations from 2021, and a larger, summarized collection of function invocations from 2019.

The data from 2021 turned out not interesting at all. After initial runs with a simple FIFO adaptation, I decided to dig more into the data and discovered that there were 119 applications in it. “Application” is Azure’s term for a deployable piece of code. This meant that the simple FIFO adaptation I created achieved 99.8% hit rate in that collection. This result was aided by the fact that early on in that dataset, almost every application has some code executing at the same time, so the minimum cache required for that experiment was large enough to be able to hold almost every application in it. This didn’t scratch my itch at all, so I went back to look at the 2019 dataset, which was harder to process because the data was all summarized, but had way more data to play with.

Hydrating the 2019 dataset

The 2019 dataset doesn’t contain invocation-by-invocation metrics. Instead, it contains percentiles of execution times for each day that was part of the data capture period. And those percentiles are actually percentiles of an average of 30 seconds of invocation-by-invocation metrics, which seems insane to me (percentiles of an average, really?). I don’t know how Azure isn’t ashamed of releasing a dataset like this, but I guess I should at least be thankful that they gave me something I could use to try to mimic production-like traffic. To use it, I needed to find a way to convert those percentiles into usable data.

Some years ago, I started writing a distributed systems simulator after a good chat with a former coworker, and I ended up needing to simulate individual metrics given some specific percentile profiles. Think of it like this: you’d give the code the p50, p90, p95, and other metrics for every component in the system, and the code would simulate individual requests back-and-forth. You’d then be able to play with the parameters to understand better about the failure conditions of the system as a whole, as well as understand which were the weakest links in it, and thus interesting targets for optimisation. I ended up not developing the simulator further (perhaps in the future!), but the code I wrote back then became useful now: I had percentiles from Azure’s dataset, and needed to come up with a way to simulate the individual invocations, so I could throw them at the different cache eviction algorithms I wanted to experiment with.

The code uses metalog distributions to go from some percentile values to a distribution that can generate values following the original percentile data. I use the bounded metalog equations to get to a quantile function, since I have the minimum and maximum metrics from the dataset.

The part that bothers me a bit is that the values I get from the distribution should be interpreted as averages rather than actual execution times, because that’s what the Azure dataset captured. I guess I could have spent more time trying to go from averages to individual values by modelling yet another distribution, but I decided to skip this and just use the averages instead. This was already production-like enough for me.

The dataset doesn’t include the disk size of any application that it runs, so I also had to improvise here: I decided to use the maximum memory usage as a silly and naive heuristic to represent the size of the code on disk. After inspecting a bit the values I got from this, I decided they were good enough for me, because it followed a distribution that I’d also expect from the size of code pieces in the system I’m developing.

Hydrating the values for every invocation turned out to be a bit tricky. The dataset contains over 12 billion invocations once you try to unwind everything! The final file (with one invocation per line) weighted over 1.2TB once the hydration code finished running.

The adaptations

I started doing this work with the plan to implement 5+ different algorithms with adaptations. I started with plain FIFO adaptations, and after some initial results I saw that it got 95%+ cache hit rates on my experiments. After implementing S3-FIFO adaptations, this number went up a bit. Those adaptations took me a few weekends of free time to finish, and by that time I started to lose interest in adding more algorithms, because my itch was already scratched: I had a pretty good idea that with the adaptations I created, the system would work sufficiently well (at least from this perspective). I could go back to focusing on finishing the system, and then think about optimising it further later, because at that point I’d have data from the system itself to experiment with.

The algorithms I started with see each item in the cache with the same singular size: if a cache has size X, it can hold X items in it. In practice, each item has a different size, so one of the adaptations I made was to use this “dynamic item size” idea in the algorithm. I came up with the term “size-aware” to identify these adaptations.

Recall that for the particular scenario I’m working with, one approach is to add items to the cache, but prevent them from being evicted while the item is in use by the machine. This constraint became a second adaptation that I made, which I named “size- and time-aware”, because items can’t be evicted from the cache for some time duration.

For “size-aware” algorithms, I coupled them with dynamic cache sizes, since I used those algorithms with the strategy of adding items to the eviction queue only after the code execution finished, and removing items from the queue if code starts executing.

Size-aware FIFO adaptation

This adaptation is straightforward:

• We start with a FIFO.
• When we want to add an item to the queue:
  1. If the queue has space to hold the item, add it and end, otherwise keep going.
  2. Remove an item from the queue.
  3. Go back to step 1.

As a consequence of this adaptation, the queue may remove more than one item before adding another.

The queue size is also dynamic, so if the queue needs to be shrunk, we just remove items from it until its total size is below the target size.

Size- and time-aware FIFO adaptation

Items have a size and a flag that indicates whether they can be removed from the queue. In my implementation, the flag is evaluated comparing the timestamp when the item “expires” and the current timestamp inside the simulation, because we know the start and end timestamps of every invocation.

When we want to add an item to the queue:

1. If the queue has space to hold the item, add it and end, otherwise keep going.
2. Remove the next item from the queue that indicates it can be removed. If we find no item like this, panic.
3. Go back to step 1.

As I mentioned in an earlier section, the queue could overfill because of the time constraint.

Size-aware S3-FIFO adaptation

In this adaptation, when we need to add an item to S3-FIFO, we ensure there is enough space by evicting as many items as needed to free up space. Everything else works the same way.

Shrinking the queue works similarly: we just evict items until its total size is below the target size.

Size- and time-aware S3-FIFO adaptation

When evicting items from S, we perform the following:

• If we can promote the item to M, we just do it.
• If we should evict to G based on the item’s frequency counter, we do so if the flag also indicates the item can be removed from the queue.
• All remaining items are forcibly promoted to M, because they have the flag indicating they can’t be removed from the queue yet.

When evicting items from M, we perform the following:

• If the item still has a positive frequency counter, we reinsert it with a decreased counter.
  • If the item has a flag indicating it can’t be removed from the queue, the counter will never drop below 1, ensuring the item remains in the cache.
• If the item has frequency counter equals to 0 and a flag allowing it to be removed, we evict it.
• If we can’t evict any items in M because of their flags, but we still need to evict, we panic.

Due to how S3-FIFO partitions its queue size into S and M, and eagerly moves things from S to M, it’s possible to run into cases where we need to insert an item into M, but M is already full of items, and none can be evicted due to the time constraint flag. Thus, the minimum size of the queue (for experiment purposes) needs to apply to M’s size instead of S3-FIFO’s size. Because of this, S3-FIFO with this adaptation needs to be bigger than its FIFO counterpart. To make things fair when evaluating S3-FIFO against FIFO, I increased the size of the FIFO queue to be the total size of S3-FIFO.

Evaluating the strategies

The following is a table of the cache hit rates of all adaptations after running on the full 1.2TB of invocation data. I used different names in the code, so to link them to the adaptations I explained in this post:

• fifo_timed is the size- and time-aware FIFO adaptation.
• s3fifo_naive_timed is the size- and time-aware S3-FIFO adaptation.
• fifo_sized is the size-aware FIFO adaptation (with dynamic queue size).
• s3fifo_naive_sized is the size-aware S3-FIFO adaptation (with dynamic queue size).

I used “naive” in the names purely because that was my first idea for an adaptation of S3-FIFO. There are multiple different adjustments that could’ve been made, and I list some of them at the end of this post.

Adaptation	Cache hit rate
fifo_timed	95.1858%
s3fifo_naive_timed	96.8998%
fifo_sized	96.5972%
s3fifo_naive_sized	96.0786%

The following graph shows the cache hit rates for different amounts of data used for the experiment. The amount of invocation data is a bit weird, as I’m measuring in disk size of the text representation of invocations instead of measuring in # of invocations, but this was just the easiest way I found to get smaller partitions of invocation data to test with.

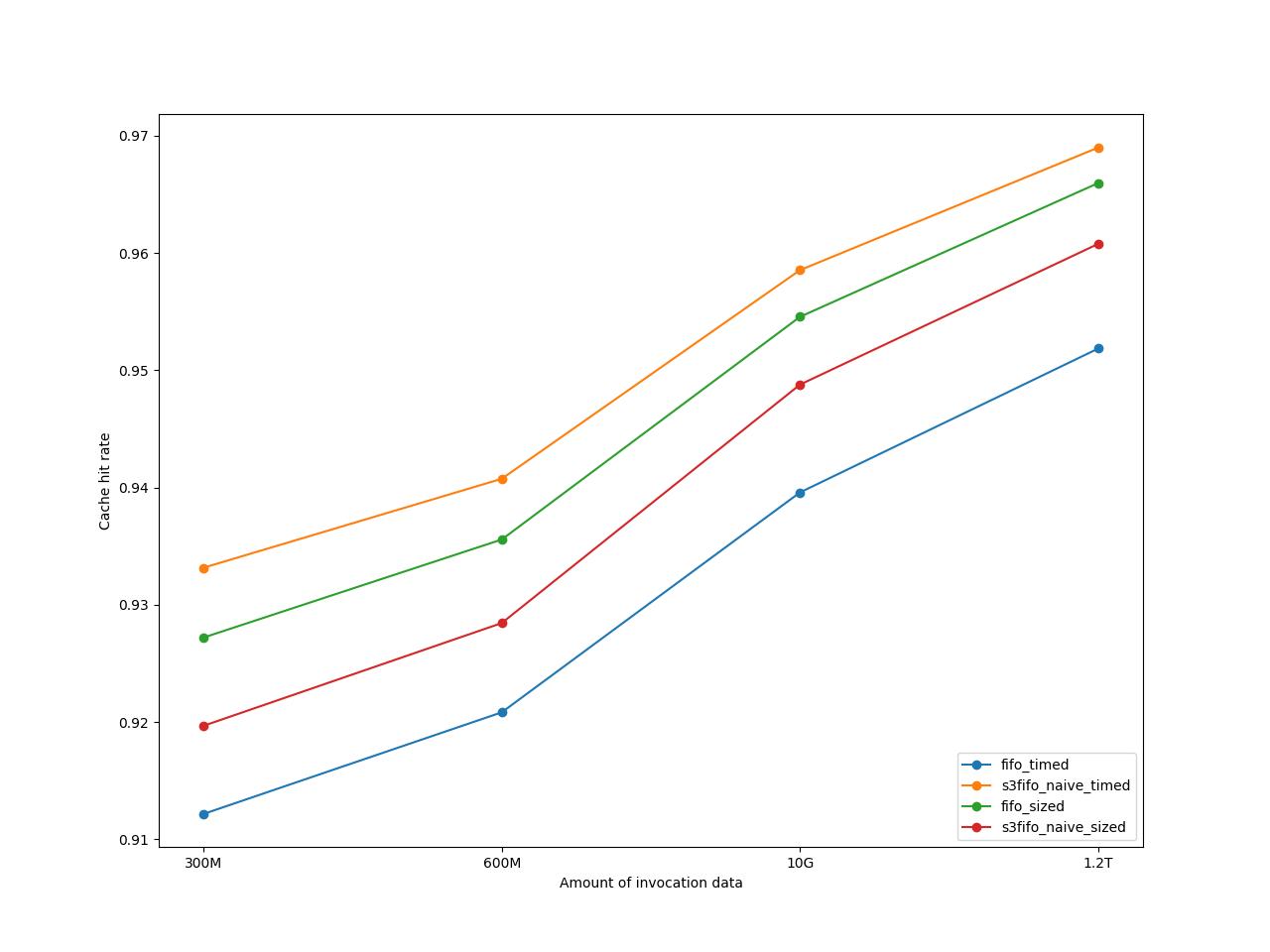
The size- and time-aware S3-FIFO adaptation ends up outperforming every other one. The size-aware FIFO adaptation is the second best approach, and given its simplicity compared to size- and time-aware S3-FIFO, I’d say it performs surprisingly well! I think that other changes to size- and time-aware S3-FIFO could improve its performance, but that’s something I haven’t done.

To understand how much the size of the cache influences the performance of the adaptations, I ran a series of experiments with varying cache sizes. I started with 1.1x the minimum cache size required for the experiment (to account for S3-FIFO’s higher cache size requirements), and ended up at 2x the minimum cache size required.

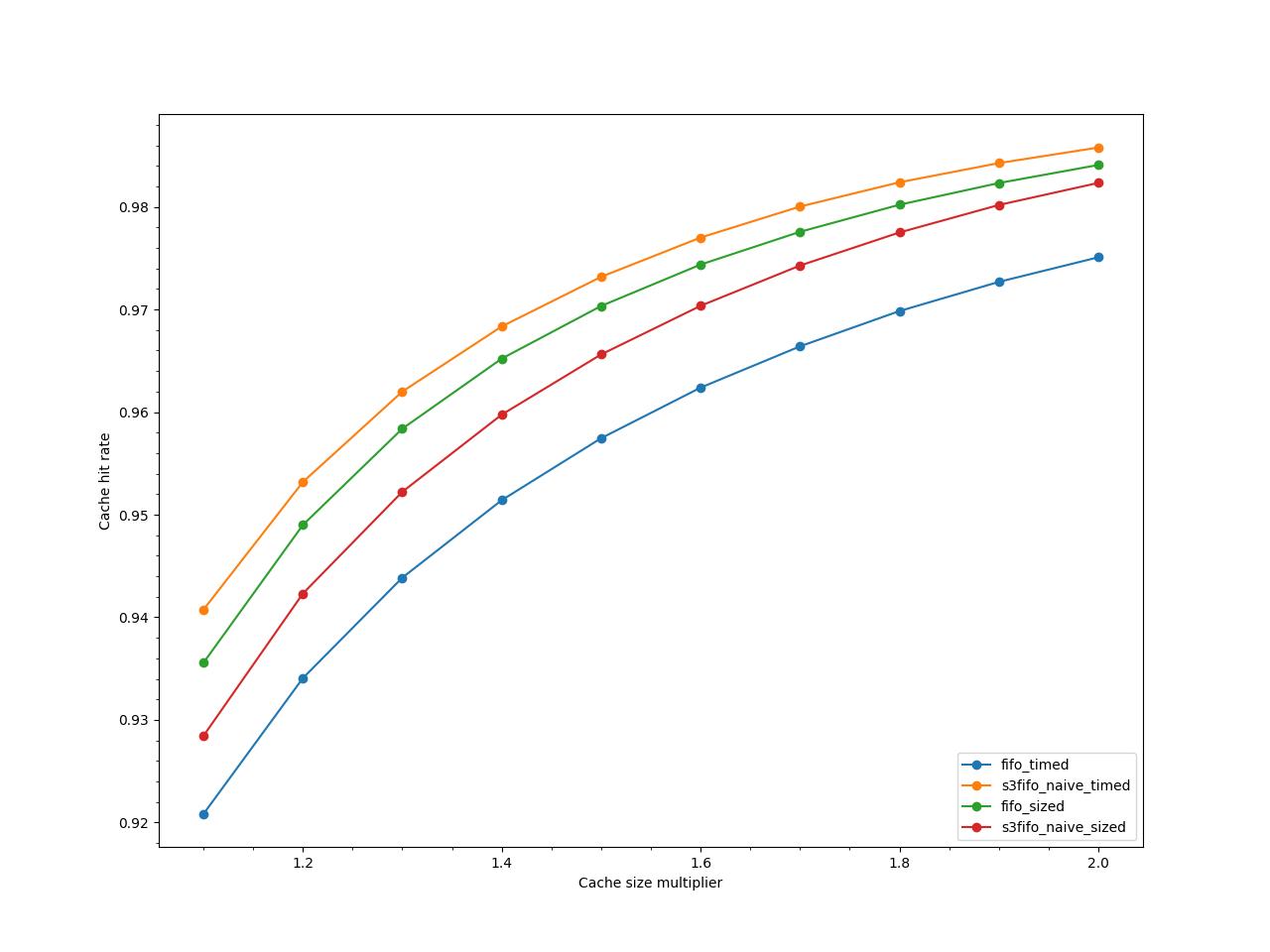
The size-aware S3-FIFO adaptation, which didn’t perform as well as the size- and time-aware one, gets a big improvement with bigger cache sizes (still not enough to beat size- and time-aware). I believe this is due to how the core S3-FIFO algorithm works. It just manages to use its queues really well.

Things for the future

For now, I’ve had fun playing with this problem and am satisfied with the solutions I found, so I’ll go back to focusing on the system as a whole. As I mentioned before, I’d like to add more algorithms to this, and still plan to do so, but only after I have a system running some traffic, so I can evaluate the algorithms on the whole system (instead of assuming just one machine running all invocations), and also evaluate on the traffic pattern that the system itself generates.

I’d also like to experiment with different adaptations of size- and time-aware S3-FIFO. Some ideas I have:

• When decreasing the frequency counter of an item during the eviction process of M, I could just not decrease at all if the item has a flag indicating it shouldn’t be removed from the queue.
• Instead of eagerly promoting from S to M the items with a flag indicating they shouldn’t be removed from the queue, I could keep them specifically in S, and only eagerly promote to M if there’s no more space in S to add more items.

If you found this interesting, would like to chat about it or chat about anything else really, feel free to drop me an email. I’m also interested in running more experiments if you find more data that fits the scenario I described in this post, so let me know if you have more data!